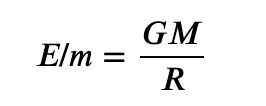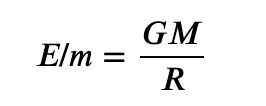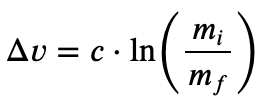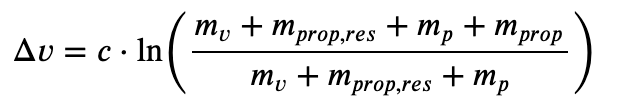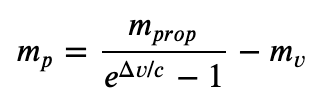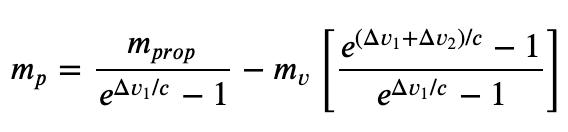Home

The moon is for having fun

The moon is made of matter. This breeds speculation: what could we do with it?

The energetic cost of removing a kilogram of stuff from some body is proportional to the mass of that body, and inversely proportional to its radius:

E

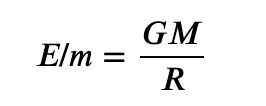
For the moon, this is about 2.8 MJ /kg; for Earth, 63 MJ / kg. That makes escaping the moon over twenty times cheaper, energetically, than escaping the Earth entirely1 - is there then a business case for exporting lunar commodities like water, oxygen, rock, or metal elsewhere in space?

No - at least, not until there is already civilization on the lunar surface. What the Earth lacks in gravitational lassitude, it more than makes up for in human population, engineering knowledge, and industrial infrastructure. This is a point Casey Handmer has made well already - this page is just a prettification of the notes I used to prove it for myself. I'll compare the cost of shipping stuff to GEO, the highest populated Earth orbit, from Earth and from the Moon.

Cost model

The cost of getting from one orbit or planet to another is driven by two things: The Δv cost is mostly determined by Keplerian physics, assuming as I will that the vehicle is firing its engines for times very short compared to the orbital periods. In this analysis I'm just going to use the values summarized in this handy map, which assume no inclination changes.

As for the propellant mass - with a piece of paper, a pen, and the conservation of momentum, you can convince yourself that the change in velocity for a nonrelativistic rocket moving freely in vacuum, ejecting propellant with a relative speed c, is

dv

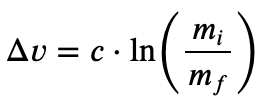
where mi is its total initial mass and mf its final mass. In terms of the dry vehicle mass mv, the payload mass mp, the propellant mass burned mprop, and the residual propellant mass mprop,res afterwards, that's

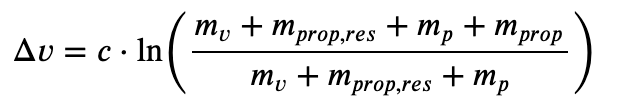
dv-breakdown

With no residual propellant, the mass breakdown of the vehicle before / after the burn looks like this:

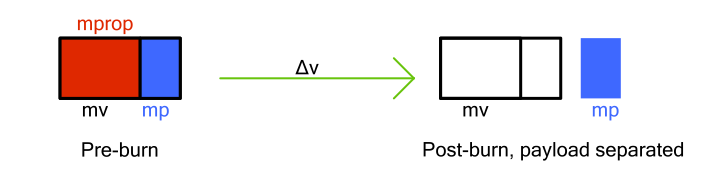
oneway

This lets us compute the payload we can carry if we fill the rocket's tanks to the brim:

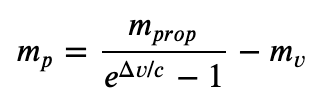
mp-1way

We'll also want to consider round trip deliveries, where the payload is the only thing that gets left at the destination:

rt

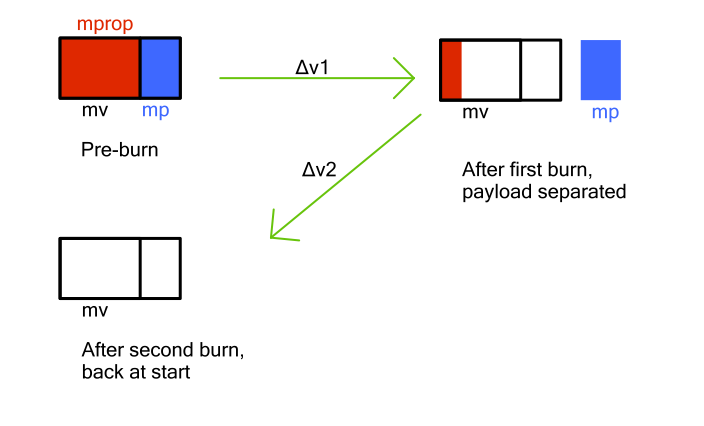
The outbound and inbound velocities Δv1 and Δv2 will differ if the start and stop states differ, or if the spacecraft passes through an atmosphere. Applying the one-way equation from above twice, you'll find that the payload capacity with a total prop mass mprop is

mp-rt

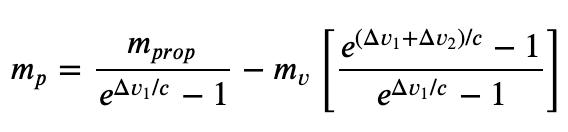
Note how you have to pay for the vehicle going both ways!

Starship specs

Until somebody decides to build a bigger one, Starship is the rocket we have to base cost considerations on, because it gives the cheapest cost per kg to orbit. Here are the numbers I'm assuming based on its wiki at the time of writing: If you assume no residual propellant and no payload, using the numbers above for Starship you get Δv = 8.9km/s; with 100 tons of payload, 6.9km/s. You can read these as an upper bound on the one-way capability of the vehicle.

I'll assume a $10M marginal cost per starship launch, which is a number Elon has thrown out that doesn't seem crazy. That corresponds to $67 / kg from Earth surface to LEO. Since we need cost estimates for flights that are not just between Earth surface and LEO, I'm going to make the simplifying assumption that cost of any Starship flight is proportional to the propellant consumed. Since the $10M flight burns 4600 tons of propellant, that means assigning a cost of about $2200 per ton of propellant used. In reality there will be operational costs that don't scale this way, but since almost all of the Starships involved in the operations described below fly with full tanks, it's not a huge source of error.

I'll also assume that lots of Starships and corresponding boosters are available, and that in-orbit refueling of Starships can be done reliably.2 That means that a Starship which expends its tanks reaching LEO from Earth surface can be refilled by 1200 / 150 = 8 starship tanker flights which carry up propellant for it. We need this capability to perform high Δv deliveries without using another spacecraft.

Delivery costs

Earth to GEO

With that preparation out of the way, we can get to dollar costs for delivery, starting with Earth to GEO as a baseline. The number we're trying to optimize is cost per ton delivered. If you look at the one-way payload equation, you see that the payload / propellant mass ratio improves as the propellant mass increases; we want to be flying starships with full tanks.

Since going from Earth surface to LEO costs a huge 9 km/s3, we need refueling in LEO to do anything useful. For a LEO -> GEO -> Earth surface trip, the outbound and return Δv requirements are Δv1 = 3.9 km/s and Δv2 = 1.47km/s, where the savings in the return comes from braking in the Earth's atmosphere. Using the Starship numbers from above, this works out to a 437 ton payload capacity to GEO. So here's how we can do GEO deliveries:

The total propellant cost is (8 + 3) booster + ship, plus 1 ship, for a total of 51,800 tons or $113M. That comes out to about $260k / payload ton.4

Earth to lunar transfer orbit

We need this for pricing one of the lunar-based schemes below. The flight plan is basically the same as going from Earth to GEO, but the outbound Δv is 3.15km/s, and the return trip is free thanks to atmospheric braking. The payload carried out by a single vehicle is about 800 tons, which requires (6 + 8) full stack launches and one ship. The cost works out to $180k/ton.

Lunar surface to GEO

Now that we understand the prices to ship things from Earth, let's compare to shipping from the Moon. What will be doing the shipping? There are a couple of obvious options: Comparing these two is enough to give us a flavor of the problem. The one way Δv cost is 4.69km/s from lunar surface to GEO, and since there's no aerobraking the return costs the same. Note that this makes the round trip voyage significantly higher Δv than one starting from LEO, which means if it is to have any hope of being competitive, the propellant has to be significantly cheaper. So, lunar exports to GEO require local propellant production.

Starship

The round trip would exceed the Starship's max Δv, so we'd have to refuel - let's say this happens in LTO, to minimize the max Δv cost the vehicle has to pay. We'll consider the two legs of the trip separately.

The Δv cost from LTO to GEO is only 2.15km/s, which means the vehicle can carry an impressive 1200 payload tons. The methane propellant, 300 tons, will have to be flown from Earth at $180k/ton. The oxidizer can have a much lower marginal cost if produced locally and brought to LTO - the question of how much lower is not important for the conclusion here, so I'll be generous and say it's free.

As for the other leg of the trip - we want to take off with a full tank of methane from the lunar surface. We'll fly a Starship down to the surface with 300 tons of methane, which requires burning about 100 tons of methane. We can then take off with a full payload, about 1100 tons, again using free lunar oxidizer. That makes about 400 tons of methane total for this leg.

So in this (crude) model, the marginal cost is set just by the methane used, which comes out to roughly $110k / ton payload in total, $150k/ton cheaper than direct Earth delivery!

However, we have to pay for the machinery used to produce thousands of tons of lunar liquid oxygen. If it costs, say, $1B all-in to set up and working, and it lasts for ten years, then we need to be shipping ($1B / 10 yr) / ($150k / ton) = 667 ton / year of payload from the lunar surface to break even.5 For comparison, a twice-a-week launch cadence for Falcon 9 carrying Starlink is about 1500 tons / year.

A different rocket

Methane imports are expensive, so what if we have a fully reusable hydrogen / oxygen-burning vehicle that gets 100% of its propellant from lunar water? I'll be generous and assume it has the same vehicle and propellant masses as Starship, but with a higher specific impulse of 465s as this RL10 engine achieves. Then the vehicle Δv budget is a whopping 10.9 km/s, and there's no refueling required in LTO! This is great, but we have to pay for the development of the rocket on top of the propellant production infrastructure. Even if that added nothing to the development cost, the difference in breakeven point is not dramatically different from the Starship case: ($1B / 10 yr) / ($250k / ton) = 400 ton / year.

In short, yes, lunar deliveries are theoretically cost competitive, if:

I'm not, like, a financial genius or anything, but even if that demand existed, this would seem like a bad deal. And if Starship isn't as cheap as I've assumed here, lunar supply doesn't become more compelling — in that case your dollars would be much better spent building a competing fully-reusable rocket in the same weight class. As long as you're going into a very difficult line of business, you may as well pick one that has revenue!

Build the base first

The fundamental point here is that, while these lunar commodities are sitting in a "cheap" gravity well, all the machinery and intelligence required to make use of them is on Earth. Our planet has the unfair advantage of an already-existing Starship program, paid for by satellite services for the people who live here, and it's optimized for traveling to Mars, not the Moon. In order for lunar exports to make sense, there has to first be a significant human presence there or nearby - almost certainly a base on the surface that drives the development of some of this infrastructure as a side effect.

To be clear, this is not any kind of chicken-and-egg problem. Putting people on the moon is a plain good idea (and with Starship, unintuitively cheap), and we should just do that first, right away. You can do all kinds of great things there, like:

Every item on this list is worth doing.6 I can't justify going to the moon to export its dirt, but I don't need to. The moon is for having fun.

1Of course, most space activity today doesn't involve escaping the Earth's gravity, but these numbers still set the scale for the difficulty of leaving the surface. The energy per kg of a LEO orbit is roughly half this. ↩

2If these assumptions aren't met, we have bigger problems than lunar commodity prices! ↩

3Note that the booster helps pay this on the way up. ↩

4It's reasonable to object that making payload transfers in orbit might be more of a pain than it's worth. An alternative plan is to fly just one starship up with 150 tons of payload, and refuel it with five tankers, which is all that's needed to get that reduced payload to GEO. That method gets you about $410k per payload ton. ↩

5If you think my cost estimates are garbage, you're right. But try your own - the required tonnage is directly proportional. ↩

6Do note that my experience of golf, while positive, is limited to a single afternoon at a driving range. I have spoken to people who have played the full game and claimed to enjoy it. I take them at their word. ↩