Starship is intended to have a one hour turnaround time on the ground between flights. With enough vehicles, you could be launching one starship every hour from a single pad, around the clock. It is interesting to think briefly about what that would look and feel like on the ground.
SpaceX’s starship overview page gives a propellant capacity (which I am assuming to be the mass used in each launch) of 3,400 tons for the first stage and 1,200 tons for the second.1
“Propellant” is the union of the liquid methane fuel and the liquid oxygen. According to this wiki, the Raptor engine burns them in a 3.6:1 mass ratio, which means that of the total 4600 ton fuel mass, 1000 tons are methane and 3600 tons are liquid oxygen.
We have already discovered at least one remarkable number. If vehicles are departing from the pad once per hour, the time-averaged (“launch-averaged”) oxygen consumption rate for the site is 3600 tons / hour, or 1 ton / second! That’s roughly a cubic meter of fluid, since the density of LOX is about 1100 kg /m3. Take a moment to picture a cube of of liquid oxygen with a meter-long side: cold, and blue, and wobbly. You have to provide one of those every second to keep this machine running, or answer the contrary at your peril.
You may be wondering, as I was, “what rate of truck deliveries of LOX would be required to support this?” Well, if a truck carries a 2m diameter cylinder that’s 20m long (numbers which I just made up, but seem reasonable), that’s roughly 60m3 per truck, so ~ 1 truck per minute.
So they’ll want to make it nearby instead. Before getting into that, let’s look at the power requirements at the vehicle.
Consider the chemical energy released in burning all those 4600 tons of propellant. Wikipedia gives the specific combustion energy of methane as about 56 MJ / kg. Now, that’s assuming you burn the fuel “stoichiometrically”, that is, matching the number of CH4 molecules and O2 molecules to consume all of them. The combustion reaction looks like this:
CH4 + 2O2 -> CO2 + 2H2O
so a stoichiometric reaction would be supplied with two oxygen molecules for every methane molecule. The rocket engine doesn’t actually do this - it runs slightly “fuel rich”, that is with a slightly smaller oxygen / methane ratio. I believe this is just to prevent the heat of the reaction from melting things in the engine. According to this wiki, Raptor uses an ox / fuel mass ratio of 3.6:1, which means a molecule ratio of 1.8:1. That means 1.8 / 2 = 90% of the fuel will be burned. The rest is just along for the ride.
Anyway, applying that 10% knockdown to the combustion energy available in the fuel, the total chemical energy released in a single launch is (fuel mass) x (specific energy) = 50,000 GJ, or about 14,000 MWh. Averaged over launches, the average combustion input power of both stages is about 14GW.
14GW! The number fairly boggles me. Other combustion processes provide a useful reference. I estimate the combustion power of gasoline car as being near 70kW while driving, so the time averaged fuel consumption of this site is equal to that of a few hundred thousand cars driving around the clock. Or, if we take a duty cycle of ~1/10 for each car, it matches the average fuel requirements of several million cars.
With that number in hand let’s turn back to the question of obtaining all that propellant.
This is a very rough estimate! If you have a better one, I’d be very interested to hear it.
There are two pieces to this: we have to get our hands on the molecules, and then cool them to the liquid form suitable for pumping into the ship.2
Let’s consider the LOX first. Happily, getting the molecules is easy as they are 20% of the atmosphere. As for cooling them, the boiling point of oxygen is 90K, so a toy model of the oxygen liquefaction system is a large refrigerator with a cold temperature of 90K, a hot temperature of 300K, and a tap attached. How much energy input is required to operate this thing? A lower on the cooling power bound can be obtained from the thermodynamic max efficiency of Tlow/ (Thot - Tlow). This is about 43% for our temperature difference. With a heat capacity of roughly 1 kJ / (kg K) (I’m ignoring factors of tens of percent there!), and then adding on the heat of vaporization, we’ll have to use at least 850 MW of power constantly to liquify our 1 ton / s of oxygen.
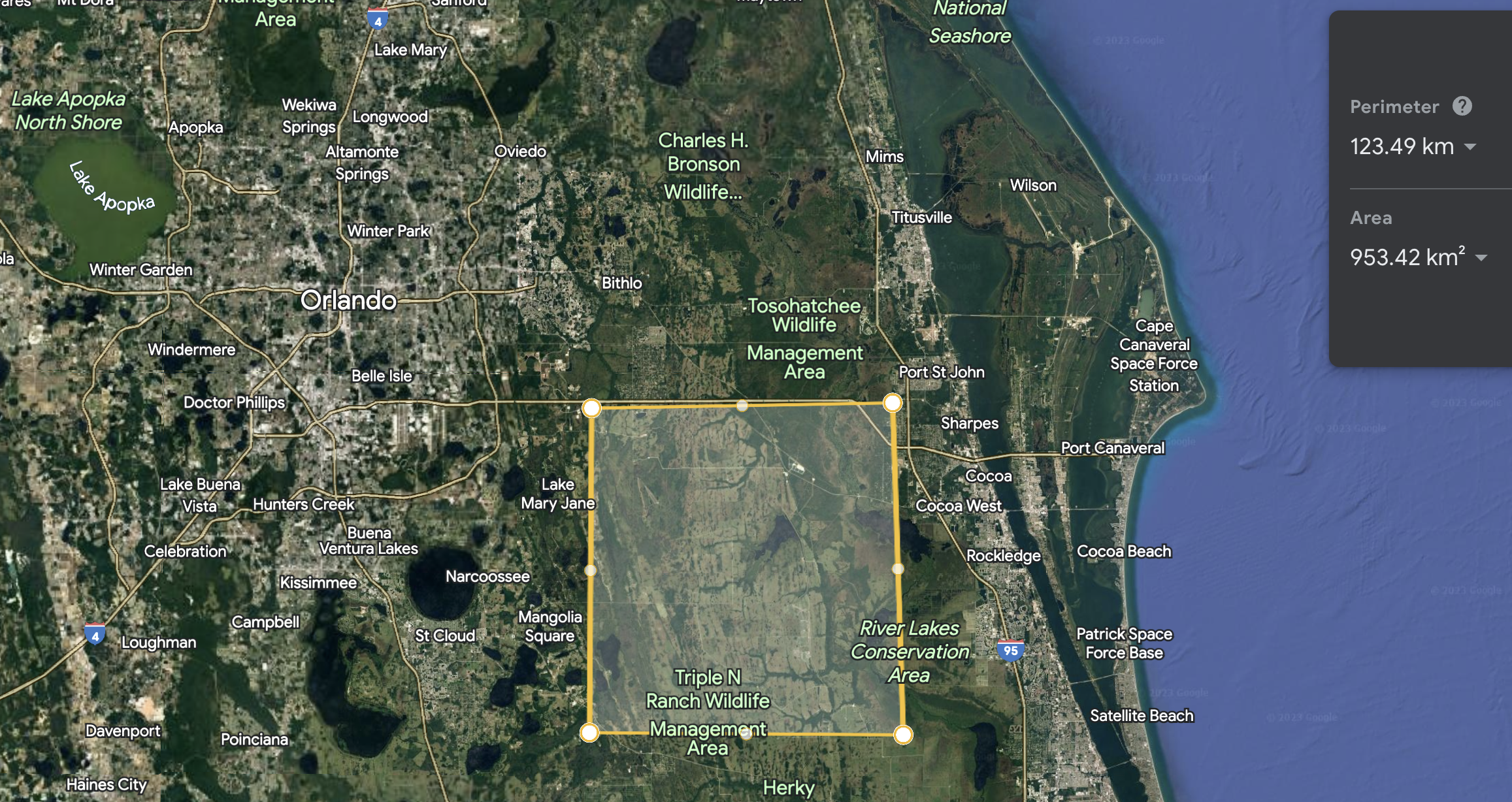
Now for the methane. One option would be to get a pipeline run to the site from a utility or even directly from some fracking site that produces natural gas. This seems like it would work,3 but means you’re strongly coupled to their fuel prices, which jump around a lot, and creating net CO2 flux into the atmosphere. A much more fun (and hopefully cheaper) option is to pull it out of the air as with the oxygen. We can buy methane generators from Terraform Industries, and run them nearby joined by a short pipeline. Assuming an efficiency of ~30% for electrical power -> methane power (is that too generous? Let me know!), we’ll need roughly 3x 14GW = 42GW of solar power to produce our fuel. Looking at this map from NREL, we can expect 5 kWH / (m2 day) of solar flux in south Florida on average, or 1kWh/(m2 day) electrical power assuming a 20% panel efficiency. That’s 42 W / m2 electrical power,4 so we’ll need roughly 109 m2 = 1000 km2 of panels, or a square 31 km on a side. Here’s what that would look like:

This would be the largest, and certainly the most amusing, solar power station on Earth. Incidentally, as the US is currently using roughly 450GW of electrical power, this site alone would account for 10%!
The cooling power required for the methane is a pittance in comparison. The heat capacity is twice as large as oxygen, but we need a lot less of it and the efficiency is a bit better, so it comes out to ~350MW.
All told, then, we should expect ~40GW of electrical power for fuel production and liquefaction, dominated by manufacturing the methane.
Let’s ignore the factors of 10% and look at the stoichiometric version of the reaction above. Roughly half of the mass goes into water, and half into CO2. The time-averaged consumption of all propellants is about 1.3 tons / sec, so we’ll get ~0.6 tons of each per second. Remembering that there are pi times ten to the seven seconds in a year, that’s ~10 Mton each of water and carbon dioxide per year. In particular, roughly 1Mton / month of water.
1 Mton / month means 106 m3 / month of water dumped into the sky at and near the launch site. If that were all to fall back down as rain on Cape Canaveral Space Force Station, which has an area of 5 km2, it would mean 200mm / month of rain, doubling the rain rate in the wettest months. Of course, a lot of that water is released at tens of kilometers of altitude and downrange, and will be able to drift around. But even so, the first, say, twenty seconds of each flight are within ~100m of the tower, yet they will consume a tenth of the first stage’s propellant mass if the first stage burn duration is three minutes.5 That water, which is deposited locally, would correspond to a solid 20 mm / month of rain, a 30% increase in the dry months.
An alien observer, who had never heard of rocket launches,6 might be forgiven for regarding the whole thing as a peculiarly periodic weather phenomenon. They’d see a largish black patch – if they made some careful measurements, they might notice a net flux of air into the patch – with some large pipes running to a pad with small forest of steel cylinders. Every hour, the pad combusts, the air gets a bit hot and moist, and a cylinder is kicked briefly out of the atmosphere. The cylinder floats back down. A little rain falls to soak the soil. The ~40 kg/s of payload delivered to orbit might only be a footnote in its journal entries!
Of course, I’m not saying anything that isn’t already “obvious” from the rocket equation and Starship’s wikipedia page. Every rocket has a small payload mass fraction. But the absolute size of the numbers matters! The combination of increase in vehicle size (~10x) and launch rate (~100x) for a rapid-launch starship site over current launch sites is large enough that previously negligible quantities suddenly leap into prominence. The launch site becomes a logistical triumph, a beast as biblically voracious and impressive as the rocket itself. Together they use as much electricity as a country7 and run a pulsed precipitation generator as an afterthought. If Starship can reach even a tenth of this rate it will be a spectactular sight.